
Orta qiymət teoremi
Orta qiymət teoremi — planar bir əyrinin üzərində seçilən hər hansısa bir hissə üzərində törəməsi (meyilliliyi) bu hissənin "ortalama" törəməsinə bərabər olan ən az bir nöqtənin var olduğunu bildirən riyazi anlayış.
Riyazi bir deyimlə, əgər f(x), [a, b] qapalı intervalında sabit və (a, b) açıq intervalında törəməsi alına bilən bir funksiyadırsa, (a, b) intervalında elə bir c nöqtəsi vardır ki,
f
′
(
c
)
=
f
(
b
)
−
f
(
a
)
b
−
a
{\displaystyle f'(c)={\frac {f(b)-f(a)}{b-a}}\,}
olur.

Bezu teoremi
Bezu teoremi —
f
(
x
)
{\displaystyle f(x)}
çoxhədlisini
(
x
−
a
)
{\displaystyle (x-a)}
ikihədlisinə bölünməsindən alınan qalıq haqqında teorem.
Teorem:
f
(
x
)
=
a
0
+
a
1
x
+
⋯
+
a
n
x
n
{\displaystyle f(x)=a_{0}+a_{1}x+\dots +a_{n}x^{n}}
çoxhədlisinin
(
x
−
a
)
{\displaystyle (x-a)}
ikihədlisinə bölünməsindən alınan qalıq bu çoxhədlinin
x
=
a
{\displaystyle x=a}
olduqda aldığı qiymətə bərabərdir.
Bezu teoremi onu ilk dəfə isbat etmiş fransız riyaziyyatçısı Eyten Bezunun (1730-1783) şərəfinə adlandırılmışdır.
== Xarici keçidlər ==
Теорема Безу и разложение многочлена на множители
Г.М. Фихтенгольц. КУРС ДИФФЕРЕНЦИАЛЬНОГО И ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ. ТОМ 1.

Fales teoremi
Fales teoremi — bucağın tərəflərini kəsən paralel düz xətlər bu bucağın bir tərəfi üzərində konqruyent parçalar ayırırsa,onda həmin düz xətlər o biri tərəf üzərində də konqruyent parçalar ayırır.A¹A²=A²A³ olarsa, B¹B²=B²B³ olar.

Kosinuslar teoremi
Kosinuslar teoremi — üçbucağın
2
{\displaystyle 2}
tərəfi və onlar arasında qalan bucaq məlum olduqda onun 3-cü tərəfinin tapılması üçün teorem.

Kouz teoremi
Kouz teoremi — transaksiya xərcləri sıfıra bərabər olduqda bazarın istənilən xarici effektin öhdəsindən gəldiyi yeni institusional iqtisadiyyatın mövqeyi.
Bu teorem ilk dəfə 1966-cı ildə Corc Stiqler tərəfindən aşağıdakı şəkildə ifadə olunmuşdur:
Stiqler tərəfindən teoremin bu cür ifadə olunması Ronald Kouzun 1960-cı ildə çap olunmuş “Sosial xərclər problemi” (ing. "The Problem of Social Cost" ) adlı məqaləyə əsaslanmışdır.
Kouz bu nəzəriyyəni istənilən fəaliyyətin bilavasitə öz iştirakçılarına deyil, üçüncü şəxslərə aid olan kənar nəticələri – eksternalların nəzərdən keçirilməsi nümunəsində sübut etmişdir.
Daha əvvəl bu problemi iqtisadçı Artur Piqu “Rifah halının iqtisadi nəzəriyyəsi” (ing. "The Economics of Welfare") kitabında nəzərdən keçirmişdir. Piquya görə, eksternallar maddi nemətlərin mənfi eksternallı təkrar istehsalına və müsbət eksternallı istehsal kəsirinə səbəb olur. O, “bazarın fiaskosu” adlandırdığı bu effektlərin neytrallaşdırılması üçün belə hallarda dövlətin iqtisadiyyata müdaxiləsini tövsiyə edirdi.
Kouz eksternalların mütləq “bazarın fiaskosu”na səbəb olması fikrini təkzib edirdi. Onun fikrinə görə, eksternallarla bağlı problemləri neytrallaşdırmaq üçün resurslara mülkiyyət hüququnun dəqiq bölgüsü və transaksiya xərclərinin mnimuma endirilməsi vacibdir.

Laplas teoremi
Laplas teoremi- determinantların minorlar üzrə ayrılışı.
TEOREM (Laplas).
n
{\displaystyle n}
-tərtibli
D
{\displaystyle D}
determinantının ixtiyari
k
{\displaystyle k}
sayda
(
1
≤
k
≤
n
−
1
)
{\displaystyle (1\leq k\leq n-1)}
sətrini (sütununu) seçib bunların nisbi vəziyyətini dəyişmədən bunlardan mümkün olan bütün müxtəlif
k
{\displaystyle k}
tərtibli minorlar düzəltsək, onda bu minorların öz cəbri tamamlayıcıları ilə hasilləri cəmi determinantın özünə bərabər olar.
İSBATI. Tutaq ki,
n
{\displaystyle n}
-tərtibli
D
{\displaystyle D}
determinantında hər hansı
i
1
,
i
2
,
.
.
.
,
i
k
{\displaystyle i_{1},i_{2},...,i_{k}}
nömrəli sətirləri qeyd edib, həmin sətirlərdən bunların nisbi vəziyyətini dəyişmədən alınan
k
×
n
{\displaystyle k\times n}
ölçülü matrisdən buradakı
α
i
1
,
α
i
2
,
.
.
.
,
α
i
k
{\displaystyle \alpha _{i_{1}},\alpha _{i_{2}},...,\alpha _{i_{k}}}
sütunlarının köməyi ilə bütün mümkün ola bilən müxtəlif
k
{\displaystyle k}
-tərtibli
M
1
,
M
2
,
.

Maslov teoremi
Maslounun ehtiyaclar iyerarxiyası (ing. Maslow's hierarchy of needs) və ya Maslou nəzəriyyəsi – 1943-cü ildə nəşr olunan bir araşdırmada amerikalı psixoloq Abraham Maslou tərəfindən təqdim edilmiş və daha sonra inkişaf etdirilmiş insan psixologiyası nəzəriyyəsidir.
Maslonun ehtiyaclar iyerarxiyası aşağıdakı kimidir:
Fizioloji tələblər (tənəffüs, qida, su, seksuallıq, yuxu, sağlam maddələr mübadiləsi, ifrazat)
Təhlükəsizlik tələbi (bədən, iş, qaynaq, əxlaq, ailə, sağlamlıq və əmlak təhlükəsizliyi)
Mənsubluğa, sevgiyə, qayğıya ehtiyac (dostluq, ailə, cinsi yaxınlıq)
Ləyaqətə ehtiyac (özünə hörmət, özünə inam, uğur, başqalarına hörmət, başqaları tərəfindən hörmət)
Özünü dərk etmə ehtiyacı (fəzilətli, yaradıcı, səmimi, problem həll edən, qərəzsiz, həqiqəti qəbul edən)
Maslow, AH (1943). İnsan motivasiyası nəzəriyyəsi. Psixoloji icmal, 50,370–396.
Maslow, AH (1965). Eupsychian İdarəetmə . Qeyd edək ki, bu kitabda yer alan Andy Kay, Kaypro'dan Andy Kaydır. Ciltli ISBN 0-87094-056-2, Ciltsiz ISBN 0–256-00353-X .
Maslow, AH (1970).
Menelay Teoremi
Menelay teoremi, transversal haqqında teorem və ya tam dördtərəfli haqqında teorem — Afin həndəsəsinin klassik teoremidir.
Bu, İskəndəriyyəli Menelaya aid edilən planimetriya teoremidir.
Əgər
A
′
,
B
′
{\displaystyle A',B'}
və
C
′
{\displaystyle C'}
nöqtələri uyğun olaraq
△
A
B
C
{\displaystyle \triangle ABC}
üçbucağının
B
C
,
C
A
{\displaystyle BC,CA}
və
A
B
{\displaystyle AB}
tərəfləri yaxud onların uzantıları üzərində olarlarsa, onda onlar yalnız və yalnız o zaman kollinear olarlar ki,
A
B
′
B
′
C
⋅
C
A
′
A
′
B
⋅
B
C
′
C
′
A
=
−
1.
{\displaystyle {\frac {AB'}{B'C}}\cdot {\frac {CA'}{A'B}}\cdot {\frac {BC'}{C'A}}=-1.}
burada
A
B
′
B
′
C
{\displaystyle {\frac {AB'}{B'C}}}
,
C
A
′
A
′
B
{\displaystyle {\frac {CA'}{A'B}}}
və
B
C
′
C
′
A
{\displaystyle {\frac {BC'}{C'A}}}
istiqamətlənmiş düz xətt parçalarının nisbətidir.

Pifaqor teoremi
Pifaqor teoremi– planimetriyada düzbucaqlı üçbucaqda tərəflər arasındakı münasibətləri ifadə edən teoremdir. Yunan riyaziyyatçısı Pifaqorun adı ilə adlandırılmışdır. Mənbələr Pifaqordan əvvəl bu teoremin başqa xalqlar tərəfindən bilindiyini göstərir. Nəzəriyyə belə ifadə olunur: Düzbucaqlı üçbucaqda katetlərin kvadratları cəmi hipotenuzun kvadratına bərabərdir.
Əgər a və b katetlər, c isə hipotenuz olarsa onda
a
2
+
b
2
=
c
2
{\displaystyle a^{2}+b^{2}=c^{2}\,}
vəya, c-ni tapmaq üçün:
c
=
a
2
+
b
2
.
{\displaystyle c={\sqrt {a^{2}+b^{2}}}.\,}
Pifaqor teoremi sahə anlayışının köməyi ilə aşağıdakı kimi ifadə olunur: Düzbucaqlı üçbucaqda hipotenuz üzərində qurulmuş kvadratın sahəsi katetlər üzərində qurulmuş kvadratların cəminə bərabərdir. Pifaqor teoreminin tərs teoremi də doğrudur. Bu teoremdə düzbucaqlı üçbucağın iki tərəfi məlum, bir tərəfi isə naməlum olur.

Puankare teoremi
Puankare teoremi isbat edilmişdir.
Puankare fərziyyəsi, sərhədi olmayan hər bir sadə bağlanmış yığcam üçölçülü manifoldun üçölçülü sferaya homeomorfik olması ilə bağlı sübut edilmiş riyazi fərziyyədir. 1904-cü ildə riyaziyyatçı Henri Puankare tərəfindən tərtib edilmiş bu fərziyyə 2002-2003-cü illərdə Qriqori Perelman tərəfindən bir sıra məqalələrdə sübut edilmişdir.
2002-ci ildə rusiyalı riyaziyyatçı Qriqori Perelman minilliyin yeddi məsələlərindən birini (mühüm riyazi problemlər, hansıların həlli on illər ərzində tapılmamışdır) isbat etmişdir. Perelman göstərmişdir ki, ilkin üçölçülü səth mütləq üçölçülü sferaya evolyusiya edəcəkdir. Bu iş üçün riyaziyyat üzrə çox dəyərli və Nobel mükafatının analoqu olan "Filds medalı" ilə təltif edilmlşdir.
Sübutun 2006-cı ildə riyaziyyat ictimaiyyəti tərəfindən təsdiqindən sonra Puankare fərziyyəsi minilliyin ilk və indiyə qədər (2024) həll edilmiş problemi oldu.
Ümumiləşdirilmiş Puankare fərziyyəsi - hər şeyin olduğu ifadəsi
n
{\displaystyle n}
- ölçülü manifold homotopiya ekvivalentidir
n
{\displaystyle n}
- ölçülü sfera yalnız və yalnız ona homeomorf olduqda.
20-ci əsrin sonlarında bu iş sübut olunmamış yeganə hal olaraq qaldı. Beləliklə, Perelmanın sübutu ümumiləşdirilmiş Puankare zənninin sübutunu da tamamlayır.

Roll teoremi
Roll teoremi — parçanın uclarında bərabər qiymətlər alan funksiyanın törəməsinin sıfırları haqqında diferensial hesabının əsas teoremi.
Teorem.
[
a
,
b
]
{\displaystyle [a,b]}
parçasında kəsilməz,
(
a
,
b
)
{\displaystyle (a,b)}
intervalında differensiallanan
y
=
f
(
x
)
{\displaystyle y=f(x)}
funksiyası
[
a
,
b
]
{\displaystyle [a,b]}
parçasının uc nöqtələrində bərabər
f
(
a
)
=
f
(
b
)
{\displaystyle f(a)=f(b)}
qiymətləri alırsa, onda
(
a
,
b
)
{\displaystyle (a,b)}
intervalında yerləşən heç olmasa bir elə
γ
{\displaystyle \gamma }
nöqtəsi var ki, bu nöqtədə funksiyanın törəməsi sıfra bərabərdir:
f
′
(
γ
)
=
0
{\displaystyle f'(\gamma )=0}
.
Funksiya
[
a
,
b
]
{\displaystyle [a,b]}
parçasında sabit olduqda teoremin doğruluğu aydındır. Bu halda
f
(
x
)
{\displaystyle f(x)}
-in törəməsi
(
a
,
b
)
{\displaystyle (a,b)}
intervalının bütün nöqtələrində sıfıra bərabərdir və
γ
{\displaystyle \gamma }
nöqtəsi olaraq istənilən nöqtəni götürmək olar.
İndi fərz edək ki,
f
(
x
)
{\displaystyle f(x)}
funksiyası sabit deyil. O,
[
a
,
b
]
{\displaystyle [a,b]}
parçasında kəsilməz olduğundan Veyerştrassın ikinci teoreminə görə özünün dəqiq aşağı
m
0
{\displaystyle m_{0}}
və dəqiq yuxarı
M
0
{\displaystyle M_{0}}
sərhədinin hər birini həmin parçanın heç olmasa bir nöqtəsində alır.
Sabit olmayan
f
(
x
)
{\displaystyle f(x)}
funksiyası üçün
m
0
<
M
0
{\displaystyle m_{0}<M_{0}}
olar və
f
(
a
)
=
f
(
b
)
{\displaystyle f(a)=f(b)}
şərtinə görə funksiya
m
0
{\displaystyle m_{0}}
və
M
0
{\displaystyle M_{0}}
sərhədlərinin heç olmasa birini parçasının daxili nöqtəsində alar.
Tutaq ki,
f
(
x
)
{\displaystyle f(x)}
funksiyası dəqiq aşağı sərhəddini daxili
γ
{\displaystyle \gamma }
nöqtəsində alır:
f
(
γ
)
=
m
0
,
(
a
<
γ
<
b
)
{\displaystyle f(\gamma )=m_{0},(a<\gamma <b)}
. Onda kifayət qədər kiçik olan ixtiyarı
|
Δ
x
|
{\displaystyle |\Delta x|}
üçün
f
(
γ
+
|
Δ
x
|
)
≥
f
(
γ
)
{\displaystyle f(\gamma +|\Delta x|)\geq f(\gamma )}
,
buradan
f
(
γ
+
Δ
x
)
−
f
(
γ
)
Δ
x
≤
0
{\displaystyle {\frac {f(\gamma +\Delta x)-f(\gamma )}{\Delta x}}\leq 0}
,
Δ
x
<
0
{\displaystyle \Delta x<0}
olduqda,
(
1
)
{\displaystyle (1)}
f
(
γ
+
Δ
x
)
+
f
(
γ
)
Δ
x
≥
0
{\displaystyle {\frac {f(\gamma +\Delta x)+f(\gamma )}{\Delta x}}\geq 0}
,
Δ
x
>
0
{\displaystyle \Delta x>0}
olduqda .

Seva Teoremi
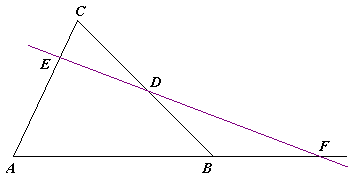
Çeva teoremi - planimetriyada üçbucaqlarla bağlı teorem. Teoremin adı italyalı riyaziyyatçı Ciovanni Çevanın adı ilə bağlıdır.
ABC üçbucağı verildiyi təqdirdə qarşı tərəfləri D, E və F-də qarşı tərəflərə qovuşdurmaq üçün AO, BO və CO sətirlərini təpələrdən ortaq O nöqtəsinə (ABC tərəflərindən birində deyil) çəkək. (AD, BE və CF seqmentləri çevianlar kimi tanınır.) Sonra imzalanmış seqment uzunluqlarından istifadə etsək,
A
F
F
B
⋅
B
D
D
C
⋅
C
E
E
A
=
1.
{\displaystyle {\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=1.}
yazarıq.
Başqa sözlə, XY uzunluğu xəttin bəzi sabit istiqamətində X -in Y-nin solunda və ya sağında olmasına görə müsbət və ya mənfi qəbul edilir. Məsələn, AF / FB, F A və B 'arasında olduqda müsbət dəyərə, əksi olsa mənfi olaraq təyin edilir.
Sinuslar teoremi
Sinuslar teoremi üçbucaqda hər bir tərəfin qarşısındakı bucağın sinusuna nisbəti olub, üçbucağın xaricinə çəkilmiş çevrənin diametrinə (radiusunun 2 misli) bərabərdir:
a
s
i
n
α
=
b
s
i
n
β
=
c
s
i
n
γ
=
2
R
{\displaystyle {\frac {a}{sin\alpha }}={\frac {b}{sin\beta }}={\frac {c}{sin\gamma }}=2R}
Burada a, b və c üçbucağın tərəflərin uzunluqları, α, β və γ isə müvafiq tərəflərin qarşısında duran bucaqlardır.
Yuxardakı bərabərliyə əsasən:
R
=
a
2
s
i
n
α
{\displaystyle R={\frac {a}{2sin\alpha }}}
Sinuslar teoremi sabit əyriliyi olan səthlərdə daha böyük ölçülərə ümumiləşdirilə bilər.

Stüart Teoremi
Stüart Teoremi Planimetriyada hər hansı bir üçbucağın daxilində bir təpədən qarşı tərəfə çəkilmiş düz xəttin uzunluğunu hesablamaq üçün teorem.

Teylor teoremi
Teylor teoremi — riyaziyyatda törəməsi bilinən bir funksiyaya bir nöqtə ətrafında, əmsalları sadəcə funksiyanın o nöqtədəki törəməsinə bağlı olan polinom şəklində ardıcıllıq əmələ gətirən nəticədir. Teorem yaxınlaşdırma hesablamalarındakı xəta payına baxmayaraq, dəqiq nəticələr də verə bilir. Bruk Teylor adlı riyaziyyatçının 1712-ci ildə etdiyi çalışmaları səbəbilə adı bu şəkildə adlanan teoremin həqiqətdə bundan 41 il əvvəl (1671-ci ildə) Ceyms Qreqori (James Gregory) tərəfindən kəşf edildiyi bilinir.
Əgər
f
(
x
)
{\displaystyle f(x)}
hər hansı a nöqtəsinin özü və onun müəyyən ətrafında (n+1)-ci tərtibə qədər törəməsi olan funksiyadırsa, x isə göstərilən ətrafdan olan
x
≠
a
{\displaystyle x\not =a}
istənilən nöqtədirsə, onda a və x nöqtələri arasında elə c nöqtəsi var ki,
f
(
x
)
=
f
(
a
)
+
f
′
(
a
)
1
!
(
x
−
a
)
+
f
″
(
a
)
2
!
(
x
−
a
)
2
+
.
.
.
.
.

Vilson teoremi
Ədədlər nəzəriyyəsində bir vacib teorem də ingilis riyaziyyatçısı C.Vilsonun (1741-1793) adı ilə bağlıdır.Teorem. İxtiyarı
p
{\displaystyle p}
sadə ədədi üçün
[
(
p
−
1
)
!
+
1
]
⋮
p
,
{\displaystyle [(p-1)!+1]\vdots p,}
yaxud
(
p
−
1
)
!
+
1
≡
0
{\displaystyle (p-1)!+1\equiv 0}
(mod
p
{\displaystyle p}
).
p
=
2
{\displaystyle p=2}
üçün teoremin doğruluğu aşkardır. Belə ki, doğrudan da:
[
(
2
−
1
)
!
+
1
]
⋮
2.
{\displaystyle [(2-1)!+1]\vdots 2.}
teoremin doğruluğu ixtiyari
p
{\displaystyle p}
sadə ədədi üçün isbat edilmişdir. Çoxhədlilər çoxluğunda müqayisələrin həlli ilə əlaqədar olan bu isbat üzərində dayanmayaraq bu teoremdən çıxan vacib bir nəticəni qeyd edək:
n
{\displaystyle n}
natural ədədinin
(
n
>
1
)
{\displaystyle (n>1)}
sadə olması üçün
[
(
n
−
1
)
!
+
1
]
⋮
n
,
{\displaystyle [(n-1)!+1]\vdots n,}
olması həm zəruri, həm də kafidir.

Viyet teoremi
Viyet teoremi və ya Viyet formulası — Çevrilmiş kvadrat tənlikdə tənliyin köklərinin hasili sərbəst həddə; köklərin cəmi isə əks işarə ilə götürülmüş əmsala (b-yə) bərabərdir. Teoremə onun əsasını qoymuş "Fransua Viyetin" adı verilib. Bu formulalar əsasən cəbrdə istifadə edilir.
Əgər
x
1
{\displaystyle x_{1}}
və
x
2
{\displaystyle x_{2}}
— kvadrat tənliyin
a
x
2
+
b
x
+
c
=
0
{\displaystyle \ ax^{2}+bx+c=0}
həlləridirsə, o zaman
{
x
1
+
x
2
=
−
b
a
x
1
x
2
=
c
a
{\displaystyle {\begin{cases}~x_{1}+x_{2}=~-{\dfrac {b}{a}}\\~x_{1}x_{2}=~{\dfrac {c}{a}}\end{cases}}}
Xüsusi halda, əgər
a
=
1
{\displaystyle a=1}
(verilən forma
x
2
+
p
x
+
q
=
0
{\displaystyle x^{2}+px+q=0}
), o zaman
{
x
1
+
x
2
=
−
p
x
1
x
2
=
q
{\displaystyle {\begin{cases}~x_{1}+x_{2}=-p\\~x_{1}x_{2}=q\end{cases}}}
Əgər
x
1
,
x
2
,
x
3
{\displaystyle x_{1},x_{2},x_{3}}
— kub tənliyinin
p
(
x
)
=
a
x
3
+
b
x
2
+
c
x
+
d
=
0
{\displaystyle p(x)=ax^{3}+bx^{2}+cx+d=0}
həlləridirsə, o zaman
{
x
1
+
x
2
+
x
3
=
−
b
a
x
1
x
2
+
x
1
x
3
+
x
2
x
3
=
c
a
x
1
x
2
x
3
=
−
d
a
{\displaystyle {\begin{cases}x_{1}+x_{2}+x_{3}=-{\dfrac {b}{a}}\\x_{1}x_{2}+x_{1}x_{3}+x_{2}x_{3}={\dfrac {c}{a}}\\x_{1}x_{2}x_{3}=-{\dfrac {d}{a}}\end{cases}}}
Viyet teoremi verilən bərabərliyi (
P
(
x
)
=
a
n
x
n
+
a
n
−
1
x
n
−
1
+
⋯
+
a
1
x
+
a
0
{\displaystyle P(x)=a_{n}x^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}}
) açmaqla isbat oluna bilər:
a
N
X
n
+
a
n
−
1
x
n
−
1
+
⋯
+
a
1
x
+
a
0
=
a
n
(
x
−
x
1
)
(
x
−
x
2
)
⋯
(
x
−
x
n
)
{\displaystyle a_{N}X^{n}+a_{n-1}x^{n-1}+\cdots +a_{1}x+a_{0}=a_{n}(x-x_{1})(x-x_{2})\cdots (x-x_{n})}
Bu isə doğrudur, çünki
x
1
,
x
2
,
…
,
x
n
{\displaystyle x_{1},x_{2},\dots ,x_{n}}
bu çoxhədlinin bütün həlləridir.

Çeva Teoremi
Çeva teoremi - planimetriyada üçbucaqlarla bağlı teorem. Teoremin adı italyalı riyaziyyatçı Ciovanni Çevanın adı ilə bağlıdır.
ABC üçbucağı verildiyi təqdirdə qarşı tərəfləri D, E və F-də qarşı tərəflərə qovuşdurmaq üçün AO, BO və CO sətirlərini təpələrdən ortaq O nöqtəsinə (ABC tərəflərindən birində deyil) çəkək. (AD, BE və CF seqmentləri çevianlar kimi tanınır.) Sonra imzalanmış seqment uzunluqlarından istifadə etsək,
A
F
F
B
⋅
B
D
D
C
⋅
C
E
E
A
=
1.
{\displaystyle {\frac {AF}{FB}}\cdot {\frac {BD}{DC}}\cdot {\frac {CE}{EA}}=1.}
yazarıq.
Başqa sözlə, XY uzunluğu xəttin bəzi sabit istiqamətində X -in Y-nin solunda və ya sağında olmasına görə müsbət və ya mənfi qəbul edilir. Məsələn, AF / FB, F A və B 'arasında olduqda müsbət dəyərə, əksi olsa mənfi olaraq təyin edilir.

Bayes teoremi
Bayes teoremi (və ya Bayes düsturu) — statistik cəhətdən bir-birindən asılı olan başqa bir hadisənin baş verməsi şərti ilə hadisənin baş vermə ehtimalını təyin etməyə imkan verən elementar ehtimal nəzəriyyəsinin əsas teoremlərindən aşağı. Başqa sözlə, Bayes düsturundan istifadə edərək həm əvvəllər məlum olan məlumatları, həm də yeni müşahidə məlumatlarını nəzərə alaraq hadisənin baş vermə ehtimalını aydınlaşdıra bilərsiniz. Bayes düsturu ehtimal nəzəriyyəsinin əsas aksiomlarından, xüsusən də şərti ehtimaldan götürülə bilər. Bayes teoreminin özəlliyi ondan ibarətdir ki, onun praktiki tətbiqi çoxlu sayda hesablamalar və hesablamalar tələb edir, ona görə də Bayes təxminləri yalnız kompüter və şəbəkə texnologiyalarında inqilabdan sonra fəal şəkildə istifadə olunmağa başladı. Bu gün o, maşın öyrənməsi və süni intellekt texnologiyalarında fəal şəkildə istifadə olunur.
Bayes teoremi yarandıqda, teoremdə istifadə edilən ehtimallar bir sıra ehtimal şərhlərinə məruz qaldı. Belə şərhlərdən biri düsturun əldə edilməsinin statistik təhlilə xüsusi yanaşmanın tətbiqi ilə bilavasitə bağlı olduğunu bildirirdi. Ehtimalın Bayesian təfsirindən istifadə edərək, teorem baş verən hadisələrin sayına görə insanın inam səviyyəsinin necə kəskin şəkildə dəyişə biləcəyini göstərir. Bayesin statistikası üçün əsas olan Bayesin gəldiyi nəticə budur. Bununla belə, teorem yalnız Bayes analizində istifadə edilmir, həm də çoxlu sayda digər hesablamalar üçün fəal şəkildə istifadə olunur.
Reqressiya teoremi
Reqressiya teoremi — pulun dəyərinin (dəyərinin) dəyərini aldıqları əmtəə və xidmətlərin izlənilməsi (“reqressiya”) ilə bağlı ifadə. Ehtimal edilir ki, müəyyən bir zamanda “obyektiv dəyəri” olan əmtəə mövcud olmuşdur, bu əmtəə müəyyən şəraitdə müəyyən sayda başqa əmtəə ilə dəyişdirilmiş və mübadilədə ekvivalent kimi istifadə olunmağa başlamışdır. İnsan emosiyalarına əsaslanan əmtəə qiymətləndirilməsinin adi üsulu ilə formalaşmışdır.
Bu bəyanatı Avstriya məktəbinin yaradıcılarından biri Lüdviq fon Mizes 1912-ci ildə özünün “Pul və kredit nəzəriyyəsi” kitabında pulun alıcılıq qabiliyyətinə malik olmasının səbəblərini izah etmək kimi tərtib etmişdir. Növbəti əsərində İnsan Fəaliyyəti. Mises teoremi Benjamin Anderson və Hovard Ellisin tənqidlərinə qarşı müdafiə edir. Özündə reqressiya teoremi pulun sosial institut kimi təkamül mənşəyi nəzəriyyəsinin ilkin olaraq Karl Menqer tərəfindən təqdim edilmiş retrospektiv tətbiqinin nəticəsidir.
Bir çox iqtisadçılar üçün alıcılıq qabiliyyətinin mənşəyinin izahı
Şiddətli dairəni qırmaq üçün Mises, pulun “dünənki” alıcılıq qabiliyyəti (əvvəlki mübadilələrdə baş verənlər) haqqında mövcud məlumatla hazırda müəyyən edilmiş qiymətə pul almağa (almağa) qərar verən şəxsin davranışını şərtləndirir. Eyni şəkildə, “dünən” pula olan tələbi “srağagün” onun alıcılıq qabiliyyəti müəyyən edirdi. Bu, sonsuzluğa qədər reqressiyaya gətirib çıxarmır, çünki əvvəllər yalnız istehsal və ya istehlaka xidmət edən qeyri-pul birjalarından pulun müəyyən bir nöqtəsi var.

Holevo teoremi
Holevo teoremi - fizika və kompüter elmlərinin fənlərarası sahəsi olan kvant hesablamaları sahəsində mühüm məhdudlaşdırıcı teoremdir. Bəzən buna Holevo bağlı deyilir, çünki teorem kvant vəziyyəti (mövcud məlumat) haqqında öyrənilə bilən məlumatların miqdarına yuxarı hədd qoyur. Teorem 1973-cü ildə Alexander Semyonoviç Holevo tərəfindən nəşr edilmişdir.
Kvant informasiya nəzəriyyəsindəki digər anlayışlarda olduğu kimi, məsələnin mahiyyətini iki nəfər arasında ünsiyyət nümunəsi ilə başa düşmək daha asandır. Bizə Alice və Bob olsun. Alis klassik təsadüfi dəyişən X-ə malikdir və müvafiq ehtimallarla {1, 2, ..., n } dəyərlərini qəbul edə bilər. {𝑝1, 𝑝2, …, 𝑝𝑛}. Alice sıxlıq matrisi ilə təmsil olunan kvant vəziyyətini hazırlayır 𝜌𝑋, dəstdən seçilir {𝜌1, 𝜌2, … 𝜌𝑛}, və bu vəziyyəti Boba ötürür. Bobun məqsədi vəziyyətin ölçülməsi ilə həyata keçirilən X dəyərini tapmaqdır 𝜌𝑋 Y ilə işarələnən klassik nəticəni verən . Bu kontekstdə mövcud informasiyanın miqdarı, yəni Bobun X dəyişəni vasitəsilə əldə edə biləcəyi məlumatın miqdarı X və Y təsadüfi dəyişənləri arasında I ( X : Y ) qarşılıqlı məlumatın bütün mümkün olan maksimum dəyəridir.

Dahi Ferma Teoremi
Bu teoremi Diofantın "Hesab" kitabının ikinci hissəsində, 8-ci məsələnin qarşısında yazmışdı: "Verilən kvadartı iki kvadrata ayırın". Başqa sözlə desək, verilmiş a ədədi üçün x2 + y2 = a2 tənliyini rasional həllərini tapmaq tələb olunur. Bu da ki bizlərə çox yaxşı tanış olan Pifaqor teoremidir və onun sonsuz sayda həlli var. Ferma qeyd etmişdir: "Kubu iki kuba, kvadratın kvadratını iki kvadratın kvadratına, ümumiyyətlə dərəcəsi ikidən böyük sonsuzluğa qədər heç bir qüvvəti bütün həmin dərəcəli iki qüvvətə ayırmaq olmaz. Mən bunun həqiqətən çox gözəl isbatını tapmışam, ama onun üçün yer olduqca azdır".
Tutaq ki, bizə belə bir məsələ verilib:
Verilmiş tam müsbət n üçün
a
n
+
b
n
=
c
n
{\displaystyle a^{n}+b^{n}=c^{n}\,\!}
düsturunu ödəyən a, b və c tam ədədlərini tapın(a, b, c>0).
Başqa sözlə xn + yn = zn qeyri-müəyyən tənliyinin n≥3 olduqda, heç bir rasiolnal həlli yoxdur. Bu təklif Fermanın böyük və ya sonuncu teoremi adlanır.
İlk baxışdan asan və ya adi görünən bu məsələ təxminən üç əsr yarım dünyanın böyük riyaziyyatçılarına meydan oxumuşdur, onun isbatını riyaziyyatçılar 350 ildən çox axtarmalı olmuşlar.
Bu məsələnin həlli Ferma Teoremi (və ya Böyük Ferma Teoremi və ya Son Ferma Teoremi) ilə bağlıdır.
Kotelnikov-Şennon teoremi
Kotelnikov-Şennon teoremi - Rəqəmsal idarəetmə sistemlərində (Digital Signal processing) diskretləşdirilən fasiləsiz siqnalı əvəz edən impulslar ardıcıllığının bərpa edilməsi üçün istifadə edilən teorem. Diskretləşdirmə intervalının qiyməti lazım olduğundan kiçik seçildikdə idarəetmə sisteminin keyfiyyətinə xələl gətirmir, lakin, izafi hesabatlara səbəb olur. Bu kəmiyyətin qiymətinin lazım olduğundan böyük seçilməsi isə məlumat itkisinə və nəticədə sistemin pisləşməsinə səbəb olur. Diskretləşdirmə intervalının qiyməti elə seçilməlidir ki, diskretləşdirilən fasiləsiz siqnal onu əvəz edən impulslar ardıcıllığından bərpa edilə bilsin.
Kroneker-Kapelli teoremi
Kroneker-Kapelli teoremi (ing. Rouché–Capelli theorem) — xətti cəbrdə teorem olub, əsas və genişlənmiş matrisləri ranqı verilmiş xətti tənliklər sistemində həllər sayını hesablamağa imkan verir. Teorem MDB məkanında Kroneker-Kapelli teoremi kimi tanınsa da, İtaliyada Rouché–Capelli teoremi, Fransada Rouché–Fontené teoremi, İspaniya və bir çox Latın Amerikası ölkələrində Frobenius teoremi kimi bilinir.
Hər hansı n dəyişənli xətti tənliklər sisteminin həlinin olması üçün onun əsas A matrisinin ranqının genişləndirilmiş [A|b] matrisinin ranqına bərabər olması zəruri və kafi şərtdir.
Tənliyin həlli olduqda:
Əgər n = rank(A) olarsa, tənliyin yeganə həlli var,
Əks halda həllər sayı sonsuz saydadır.
Matris
Leopold Kroneker
A. Carpinteri. Structural mechanics. Taylor and Francis. 1997. səh.

Xan-Banax teoremi
Tutaq ki,
p
{\displaystyle p}
funksionalı
E
{\displaystyle E}
həqiqi xətti fəzasında təyin olunmuş bircins qabarıq funksional,
f
{\displaystyle f}
isə müəyyən
L
⊂
E
{\displaystyle L\subset E}
xətti altfəzasında təyin olunmuş və
istənilən
x
∈
L
{\displaystyle x\in L}
ünsürü üçün
f
(
x
)
≤
p
(
x
)
{\displaystyle f(x)\leq p(x)}
şərtini ödəyən həqiqi xətti funksionaldır. Onda
f
{\displaystyle f}
funksionalını
bütün
E
{\displaystyle E}
fəzasında təyin olunan və istənilən
x
∈
E
{\displaystyle x\in E}
ünsürü üçün
F
(
x
)
≤
p
(
x
)
{\displaystyle F(x)\leq p(x)}
şərtini ödəyən
F
{\displaystyle F}
həqiqi xətti funksionalına davam etdirmək olar.
f
{\displaystyle f}
funksionalının hər bir
x
∈
D
(
f
′
)
{\displaystyle x\in D(f^{\prime })}
ünsürü üçün
f
′
(
x
)
≤
p
(
x
)
{\displaystyle f^{\prime }(x)\leq p(x)}
bərabərsizliyini ödəyən bütün
f
′
{\displaystyle f^{\prime }}
xətti davamları
çoxluğunu
F
p
{\displaystyle F_{p}}
ilə işarə edək. Burada
D
(
f
′
)
{\displaystyle D(f^{\prime })}
f
′
{\displaystyle f^{\prime }}
funksionalının
təyin oblastıdır.
f
1
′
,
f
2
′
∈
F
p
{\displaystyle f_{1}^{\prime },f_{2}^{\prime }\in F_{p}}
funksionallarından
f
2
′
{\displaystyle f_{2}^{\prime }}
funksionalı
f
1
′
{\displaystyle f_{1}^{\prime }}
-in davamı olduqda bunu
f
1
′
<
f
2
′
{\displaystyle f_{1}^{\prime }<f_{2}^{\prime }}
şəklində
ifadə edək. Onda
F
p
{\displaystyle F_{p}}
bu münasibətə nəzərən qismən nizamlanmış çoxluq olar. Əgər
F
p
′
{\displaystyle F_{p}^{\prime }}
-lə
F
p
{\displaystyle F_{p}}
-nin (xətti) nizamlanmış hissəsini işarə etsək,
⋃
f
′
∈
F
p
D
(
f
′
)
{\displaystyle \bigcup \limits _{f^{\prime }\in F_{p}}D(f^{\prime })}
çoxluğunda təyin olunan və hər bir
x
∈
D
(
f
′
)
{\displaystyle x\in D(f^{\prime })}
,
f
′
∈
F
p
′
{\displaystyle f^{\prime }\in F_{p}^{\prime }}
üçün
f
0
(
x
)
=
f
′
(
x
)
{\displaystyle f_{0}(x)=f^{\prime }(x)}
kimi verilən
f
0
{\displaystyle f_{0}}
funksionalı
F
p
′
{\displaystyle F_{p}^{\prime }}
çoxluğunun yuxarı sərhəddi olacaqdır. Bu da onu göstərir ki,
F
p
{\displaystyle F_{p}}
çoxluğu Sorn lemmasının şərtlərini ödəyir. Onda bu lemmaya görə
F
p
{\displaystyle F_{p}}
çoxluğu
F
{\displaystyle F}
maksimal ünsürünə malikdir. Asanlıqla görmək olar ki,
f
{\displaystyle f}
maksimal funksionalının təyin oblastı bütün
E
{\displaystyle E}
oblastı ilə üst-üstə düşür.